Мы используем файлы cookie.
Продолжая использовать сайт, вы даете свое согласие на работу с этими файлами.

معادلة يونغ لابلاس

Другие языки:

معادلة يونغ لابلاس

Подписчиков: 0, рейтинг: 0

معادلة يونغ لابلاس في الفيزياء هي معادلة جبرية تصف فرق الضغط الشعري المستدام عبر الواجهة بين سائلين ساكنين، مثل الماء والهواء، بسبب ظاهرة التوتر السطحي أو توتر الجدار، على الرغم من أن استخدام الأخير لا يمكن تطبيقه إلا إذا افترضنا أن الجدار رقيق جدًا. ترتبط معادلة يونغ لابلاس باختلاف الضغط بشكل السطح أو الجدار وهي مهمة بشكل أساسي في دراسة الأسطح الشعرية الثابتة. إنه بيان لتوازن الضغط الطبيعي للسوائل الثابتة التي تلتقي في واجهة، حيث يتعامل مع الواجهة كسطح (سماكة صفرية):

{\begin{aligned}\Delta p&=-\gamma \nabla \cdot {\hat {n}}\\&=-2\gamma H_{f}\\&=-\gamma \left({\frac {1}{R_{1}}}+{\frac {1}{R_{2}}}\right)\end{aligned}}

حيث p∆ هو ضغط لابلاس، فرق الضغط عبر واجهة المائع (الضغط الخارجي مطروحًا منه الضغط الداخلي)، 𝛾 هو التوتر السطحي (أو توتر الجدار)، 𝑛 هي الوحدة العادية التي تشير إلى السطح، Hf هو المتوسط الانحناء، وR1 وR2 هما نصف القطر الأساسي للانحناء. لاحظ أنه يُأخذ الضغط الطبيعي فقط في الاعتبار، وذلك لأنه يُثبَت أن السطح البيني الثابت ممكن فقط في حالة عدم وجود إجهاد عرضي.

سُمِّيَت المعادلة على اسم توماس يونغ، الذي طور النظرية النوعية للتوتر السطحي في عام 1805، وبيير سيمون لابلاس الذي أكمل الوصف الرياضي في العام التالي. يطلق عليها أحيانًا أيضًا معادلة يونغ لابلاس- غاوس، حيث وحد كارل فريدريش غاوس عمل يونغ ولابلاس في عام 1830، مستمدًا كلاً من المعادلة التفاضلية وشروط الحدود باستخدام مبادئ العمل الافتراضية ليوهان برنولي.

أفلام الصابون

إذا كان فرق الضغط صفراً، كما هو الحال في فيلم صابون بدون جاذبية، فستتخذ الواجهة شكل الحد الأدنى من السطح.

مستحلبات

تشرح المعادلة أيضًا الطاقة المطلوبة لإنشاء مستحلب. لتشكيل قطرات صغيرة منحنية للغاية من المستحلب، يلزم طاقة إضافية للتغلب على الضغط الكبير الناتج عن نصف قطرها الصغير.

يتسبب ضغط لابلاس، الذي يكون أكبر بالنسبة للقطرات الأصغر، في انتشار الجزيئات من أصغر القطرات في المستحلب ويؤدي إلى تقشر المستحلب عبر إنضاج أو ستوالد.

ضغط الشعيرات الدموية في أنبوب

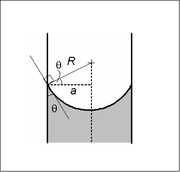
هلالة كورية مع زاوية ترطيب أقل من ٩0درجة

: في أنبوب ضيق بدرجة كافية ( سندات منخفض) من مقطع عرضي دائري (نصف قطر أ)، تشكل الواجهة بين سائلين هلالة تمثل جزءًا من سطح كرة بنصف قطر R. يقفز الضغط عبر هذا السطح يرتبط بنصف القطر والتوتر السطحي y بواسطة

\Delta p={\frac {2\gamma }{R}}.

يمكن إظهار ذلك من خلال كتابة معادلة يونغ لابلاس في شكل كروي مع شرط حد زاوية الاتصال وأيضًا شرط حد ارتفاع محدد في، على سبيل المثال، أسفل الغضروف المفصلي. الحل هو جزء من كرة، وسيكون الحل موجودًا فقط لفرق الضغط الموضح أعلاه. هذا مهم لأنه لا توجد معادلة أو قانون آخر لتحديد فرق الضغط ؛ إن وجود حل لقيمة محددة واحدة لفرق الضغط يتطلب ذلك.

سيكون نصف قطر الكرة دالة فقط لزاوية التلامس، θ، والتي تعتمد بدورها على الخصائص الدقيقة للسوائل ومادة الحاوية التي تتلامس / تتفاعل معها السوائل المعنية:

R={\frac {a}{\cos \theta }}

بحيث يمكن كتابة فرق الضغط على النحوالتالي:

\Delta p={\frac {2\gamma \cos \theta }{a}}.

رسم توضيحي لارتفاع الشعيرات الدموية. أحمر = زاوية تلامس أقل من 90 درجة ؛ أزرق = زاوية تلامس أكبر من 90 درجة

من أجل الحفاظ على التوازن الهيدروستاتيكي، يتم موازنة الضغط الشعري المستحث عن طريق تغيير الارتفاع، h، والذي يمكن أن يكون موجبًا أو سالبًا، اعتمادًا على ما إذا كانت زاوية الترطيب أقل أو أكبر من 90 درجة. للحصول على سائل من كثافة ρ:

\rho gh={\frac {2\gamma \cos \theta }{a}}.

حيث g هي عجلة الجاذبية. يُعرف هذا أحيانًا باسم قانون جورين أو ارتفاع جورين بعد جيمس جورين الذي درس التأثير في عام 1٧18

بالنسبة لأنبوب زجاجي مملوء بالماء في الهواء عند مستوى سطح البحر:

y=0.0728J/m2at 20 °C

θ=20°(0.35rad)

ρ=1000kg/m3

g=9.8m/s2

ومن ثم يعطى ارتفاع عمود الماء من خلال:

h\approx {{1.4\times 10^{-5}}\mathrm {m}  \over a}.

في حالة الأنبوب الذي يبلغ عرضه 2 مم (نصف قطره 1 مم)، سيرتفع الماء 14 مم. ومع ذلك، بالنسبة للأنبوب الشعري نصف قطره 0.1 مم، سيرتفع الماء 14 سم (حوالي 6 بوصات).

ملف:YoungLaplace example drop.gif

ملف:YoungLaplace example bridge.gif

عمل الشعيرات الدموية بشكل عام

في الحالة العامة، بالنسبة لسطح حر وحيث يوجد "ضغط زائد" مطبق، Δp، عند السطح البيني في حالة توازن، يوجد توازن بين الضغط المطبق والضغط الهيدروستاتيكي وتأثيرات التوتر السطحي. تصبح معادلة يونج لابلاس:

\Delta p=\rho gh-\gamma \left({\frac {1}{R_{1}}}+{\frac {1}{R_{2}}}\right)

يمكن أن تكون المعادلة غير ذات أبعاد من حيث مقياس الطول الخاص بها، الطول الشعري:

L_{c}={\sqrt {\frac {\gamma }{\rho g}}},

والضغط المميز

p_{c}={\frac {\gamma }{L_{c}}}={\sqrt {\gamma \rho g}}.

وللحصول على مياه نظيفة عند درجة حرارة وضغط قياسيين، يبلغ طول الشعيرات الدموية حوالي 2 مم. ثم تصبح المعادلة غير الأبعاد:

h^{*}-\Delta p^{*}=\left({\frac {1}{{R_{1}}^{*}}}+{\frac {1}{{R_{2}}^{*}}}\right).

وبالتالي، يتم تحديد شكل السطح بواسطة معلمة واحدة فقط، ويتم تحديد الضغط الزائد للسائل، Δp* ومقياس السطح بواسطة طول الشعيرات الدموية. يتطلب حل المعادلة شرطًا أو ليًا للموضع وتدرج السطح عند نقطة البداية.

المعادلات المحورية

يمكن العثور على الشكل (غير الأبعاد) r (z) لسطح متماثل المحور عن طريق استبدال التعبيرات العامة للانحناءات الرئيسية لإعطاء معادلات يونغ لابلاس الهيدروستاتيكي r

${\frac {r''}{(1+r'^{2})^{{3}/{2}}}}-{\frac {1}{r(z){\sqrt {1+r'^{2}}}}}=z-\Delta p^{}$ ${\frac {z''}{(1+z'^{2})^{3/2}}}+{\frac {z'}{r(1+z'^{2})^{{1}/{2}}}}=\Delta p^{}-z(r).$ التطبيق في الطب

في الطب، غالبًا ما يشار إليه باسم قانون لابلاس، ويستخدم في سياق فسيولوجيا القلب والأو عية الدموية، وأيضًا فيزيولوجيا الجهاز التنفسي، على الرغم من أن الاستخدام الأخير غالبًا ما يكون خاطئا

تاريخ

أجرى فرانسيس هوكسبي بعضًا من أو ائل الملاحظات والتجارب في عام 1709 وتكرر ذلك في عام 1718 بواسطة جيمس جورين الذي لاحظ أن ارتفاع السائل في عمود شعري كان دالة فقط في منطقة المقطع العرضي على السطح، وليس من أي أبعاد أخرى للعمود.

وضع توماس يونغ أسس المعادلة في مقالته المنشورة عام 1804 بعنوان "مقال عن تماسك السوائل" حيث حدد بعبارات وصفية المبادئ التي تحكم الاتصال بين السوائل (جنبًا إلى جنب مع العديد من الجوانب الأخرى للسلوك السائل). تبع بيير سيمون لابلاس هذا الأمر في Mécanique Céleste مع الوصف الرياضي الرسمي المذكور أعلاه، والذي أعاد إنتاج العلاقة التي وصفها يونغ من قبل بمصطلحات رمزية.

قبل لابلاس الفكرة التي طرحها هوكسبي في كتابه تجارب فيزيائية ميكانيكية (1709)، مفادها أن هذه الظاهرة كانت ناتجة عن قوة جذب غير محسوسة على مسافات معقولة. الجزء الذي يتعامل مع تأثير مادة صلبة على سائل والعمل المتبادل بين سائلين لم يتم تنفيذه بشكل كامل، ولكن في النهاية تم إكماله بواسطة كارل فريدريش جاوس. قدم فرانز إرنست.قدم فرانز إرنست نيومان (1798-1895) لاحقًا بعض التفاصيل

قراءات إضافية

Maxwell, James Clerk; Strutt, John William (1911). "Capillary Action" . In Chisholm, Hugh (ed.). Encyclopædia Britannica (بالإنجليزية) (11th ed.). Cambridge University Press. Vol. 5. pp. 256–275.
Batchelor, G. K. (1967) An Introduction To Fluid Dynamics, Cambridge University Press
Jurin, J. (1716). "An account of some experiments shown before the Royal Society; with an enquiry into the cause of the ascent and suspension of water in capillary tubes". Philosophical Transactions of the Royal Society. ج. 30 ع. 351–363: 739–747. doi:10.1098/rstl.1717.0026. S2CID 186211806. مؤرشف من الأصل في 2017-10-20.
Tadros T. F. (1995) Surfactants in Agrochemicals, Surfactant Science series, vol.54, Dekker